Computing Life

数码相机可以对远处的物体进行对焦。那能不能用来测量到物体的距离呢？

理论上是可以的，用相机对焦，使得待测量的景物合焦，然后从镜头的距离标尺上读出距离就可以了。但这种方法只对近处的物体有效，对远处的物体精度非常低。但如果退一步想，我们有没有可能跳出数码相机的框框，还是用一样的原理，用更牛逼的设备比如更大口径的镜头（景深更浅）来实现这个思路呢？本质上这是一种被动测距的方法，不会被被测物体发现（比如雷达枪测速会被司机装的雷达探测器发现，接着就是一脚刹车），基本不需要能量。如果可以做的小+精度高的话是非常吸引人的。这个文章首先介绍几种常见的基于这个思路的测量方法，然后做一些定量计算，最后给出建议的方案。因为很多公式我也是第一次推导，所以如果有错出还望不吝指出。

从原理上说，测距就是把距离转换成一个和距离一一对应的物理量，测量这个物理量就可以得到距离。一个例子是激光测距 (time of flight)，就是把距离转换成时间。从纯摄影的角度来说，从相机的原理出发，有三种测距的方法：黄斑测距，裂像测距和峰值测距。（这里叫xx测距而不说xx对焦主要是因为对焦其实是后一步的额外动作。如果用过上古时代的相机比如Leica III的话，会有经验对焦需要分为两步，第一步是先用单独的测距仪比如黄斑测距仪测出距离，然后把镜头转到对应的距离上，就完成了对焦。现代相机用的都是联动的对焦装置，所以对焦一步就好了。）在引入计算机以后，从计算摄影学和机器视觉的角度出发，我们又多了三种测距的方法，双目测距，散斑测距，和激光测距。当然峰值测距也是数码相机时代以后才有的产物，所以它也是机器视觉的一个领域，叫depth from defocus。

首先我们来看看经典的黄斑测距。徕卡M系列相机用的就是黄斑测距，它的使用体验是，在取景对焦器里面有一个明亮的黄斑，和正常看出去的景物形成一个重影。拧动对焦环会改变这个重影的位置。当这个重影和实际的景物重合的时候就合焦了。从原理上来说这个其实应该叫视差测距。如下图所示，一个景物发出的光（红色）通过两个不同的窗口被一个半透半反镜聚合到同一个目镜里。因为这两个窗口之间有距离，所以两束红色的光的角度存在着微小的差异。这个差异被光学器件放大之后，就表现为两个不重合的像。当调整一个反射五棱镜的时候，从右侧窗口进入的光线形成的像会左右偏移。不同的调整角度对应着不同的距离，那么当两个像重合的时候，就可以直接读出距离了。

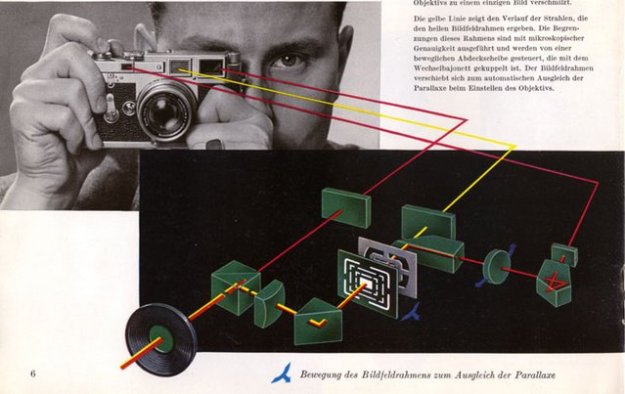
徕卡相机的黄斑联动对焦原理图，图片来自来自http://leicaphilia.com/how-a-rangefinder-works/

这种方法不依赖于镜头本身，体积可以做的很小巧。但从原理上也可以看出，它的精度非常依赖于两个窗口之间的距离（叫做基线长度）。基线越长，一方面左右两束光线相差的角度越大，一方面这个相差的角度也会更显著地体现在黄斑像的位置偏移上。如下图所示，在物距d远大于基线长度l的时候，可以简单计算出人观察到的黄斑偏移量是$l^2/d$。考虑到人是通过目镜观察这个偏移的，所以还需要乘以一个目镜放大倍率$\lambda$，得到$\lambda l^2 / d$。

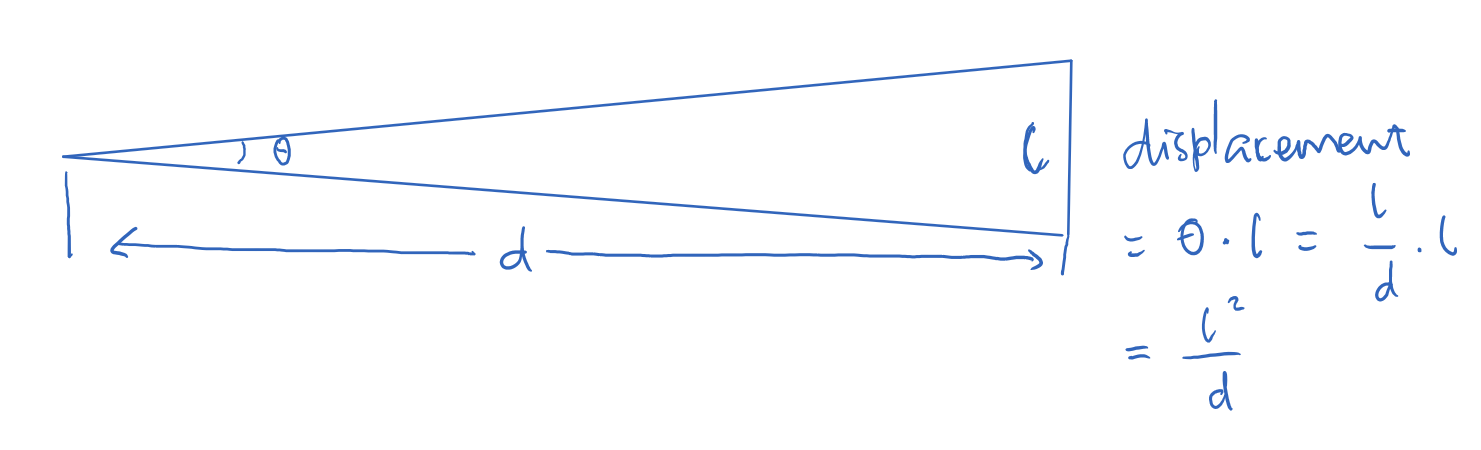
黄斑测距精度的理论推导

那这个机制的精度如何呢？这个精度是有两个部分局限的。首先是人眼的角分辨率。人眼的角分辨率约为一角分，考虑到半透半反镜到人眼的距离一般不超过5cm，所以这个黄斑的偏移量在小于0.015mm的时候人就看不到它的移动了。代入前面的公式，可以得到$\lambda l^2 / d >= 0.015mm$，也就是这个d的量程上界是$\lambda l^2 / 0.015mm$。比如徕卡M6 0.85版相机，基线长度l约为5cm，放大倍率0.85，那么有效量程d就是1.6km。看上去这是个非常反直觉（过大）的答案，但要注意这里量程仅仅考虑了光学，也就是说如果d从1.6km挪动到16km甚至160km，人眼看上去黄斑完全没有任何变化。实际上还有另一个限制因素在机械上。

从机械的角度来说，当d是1.6km的时候，可以算出来张角\theta是0.000031弧度，如果把测距的量程下界设为0.7m，此时$\theta=0.071$弧度，也就是说这个测距仪的反射镜的角度需要在0.000031~0.071弧度之间调整，通过机械结构测量具体的角度，然后把它换算成距离。这个要求看上去很高，但其实同光学上我们用了l作为杠杆来增大黄斑的移动距离一样，我们也可以用齿轮等结构来放大角度。比如上述相机配套的50mm镜头的对焦行程大约是120度（2.09弧度），这大约就把反射镜的角度放大了30倍。我不是特别清楚人手拧动的精度可以到多少，这里为了分析简便先取1度好了（不对再改）。也就是说手拧了1度（0.017弧度），反射镜只动了0.00058弧度。这个0.00058弧度可不得了。考虑到$\theta = l / d$，当$\theta$在上限0.071弧度的时候，偏转0.00058弧度意味着距离的刻度跑了5.8mm，相对误差0.8%（这个值比50mm f/1.4镜头在该处的景深还是要小的）；当\theta在下限0.000031弧度的时候，差了0.00058弧度就差了。。1.5km。。相对误差95%。。从数学的角度来看，把前面的公式稍微整理一下，这个相对误差可以写成$|d_2 - d_1| / d = (l / \theta - l / (\theta + \delta \theta)) / (l / \theta) = \delta \theta / ( \theta + \delta \theta)$. 画个图的话长这样：

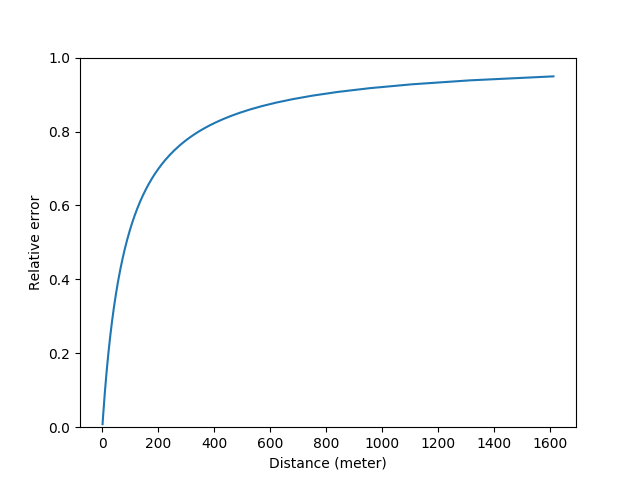
如果我们认为有效量程指的是相对误差不超过5%的话，那么$\theta$需要大于$19\delta \theta$，对应的距离就是4.5m。这是一个数量级符合直觉的答案，和相机镜头上的标尺相符。注意相机测距只是为了对焦，在物距比较远的情况下，即使相对误差比较大，对合焦的影响也不是很大。那么回到题主的问题，如果我们想测量比如1公里外的物体的距离，应该怎么办呢？有两种方法，增加基线的长度，增加对角度调整的精细度。比如我们用一个长度为20cm的基线来取代原来的5cm的基线，这时1公里外的物体的$\theta$就从0.000031弧度变成了0.0002。然后我们再用一个直径50cm的对焦手轮代替直径5cm的镜头对焦环，以及更长的对焦行程比如这个手环可以转3圈（1080度）来代替镜头的120度。此时我们就有了2700倍的角度放大而不再是30倍的放大倍率。所以相应的$\delta \theta$也减小到了0.0000064弧度。这时候再算5%相对误差的有效量程的话，可以得出真·1.6km的量程。这时候用来测量云高就比较靠谱了。当然50cm的手轮配20cm的基线看起来头重脚轻，有兴趣的同学可以进一步推导看看从设计和人体工学的角度什么样的参数设置比较合理。

下面我们来看剩下的另一种传统对焦的方法，裂像测距/对焦。对单反/双反相机而言，光线透过镜头（不论是单反的taking lens还是双反的viewing lens）打在毛玻璃上。毛玻璃上有一个光楔结构（wedge prism，就是顶角很小的三棱镜，长得如下图所示），可以对光线产生偏转。光楔因为顶角非常小，所以色散几乎观察不到，而主要用来对光线进行偏折，改变它行进的方向。

裂像屏上的光楔。下文的分析针对的是两个光楔的情况。图片来自https://www.zhihu.com/question/40608644

具体的原理很好理解。如下图所示，假如有一个和纸面垂直的棍子从透镜左侧发出两束光，一束如蓝色所示的光经过镜头的上部到达焦平面，一束如红色所示的光经过镜头的下部到达焦平面。焦平面上面镶嵌了两个光楔，离我们近的一个用蓝色表示，离我们远的用红色表示。首先当对焦是准确的时候，物体发出的光聚焦在对焦屏上，如下图中间一行所示。这个时候因为光线经过光楔的中心，所以红蓝光楔出来的光线是相同角度的，我们看到的就是这个线是对齐的。注意在看这个图的时候要想象所有的光线其实都是一个垂直于纸面的光带。

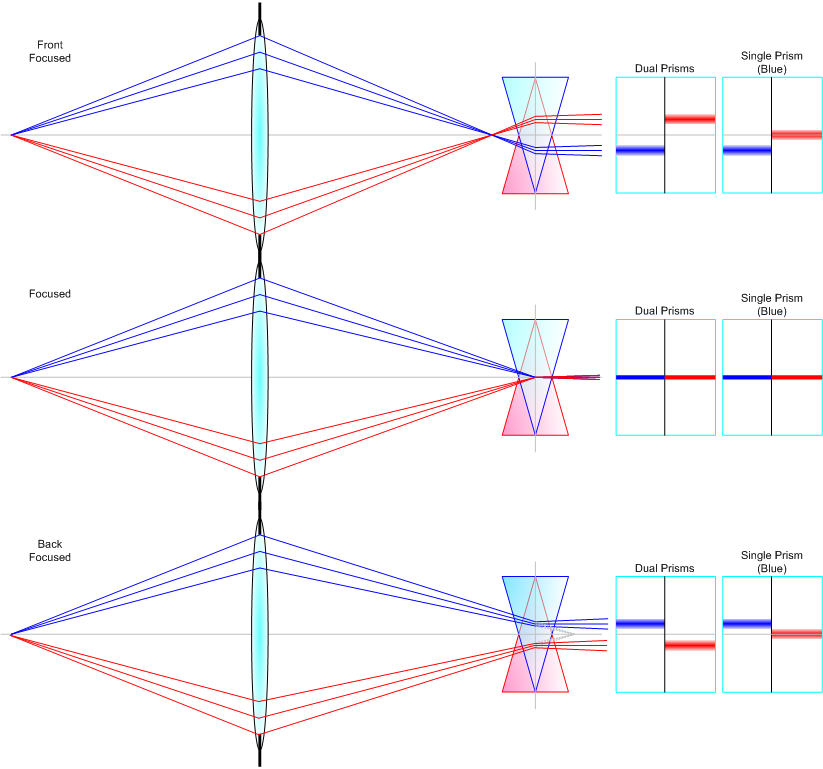
裂像对焦屏的原理。图片来自https://www.pointsinfocus.com/learning/cameras-lenses/brief-history-focusing/

当对焦不准的时候，比如当焦平面在对焦屏前方的时候（如上图第一行所示）。此时屏幕左侧的光经过蓝色的光楔会向上偏折并发散，对观察对焦屏的人眼而言形成一个镜后的虚像。从焦平面和对焦屏的相对位置可以看出，这个虚像的位置是在中线的下方，这是为什么右边人眼视角的示意图中蓝线在中线下方。与此同时，其实红色的光也会被蓝色光楔偏折（图中未绘出），但因为它的方向本来就偏上，偏折后会大幅向上，所以人眼观察不到。和蓝色光线被蓝色光楔偏折的道理相同，红色的光经过红色光楔偏折后会在右侧红色光楔前方（对人眼而言是镜后）形成一个虚像。此时人眼看上去屏幕右侧的红线就上移了。对于焦平面在对焦屏后方的分析如上图第三行所示，就不重复分析了。如果回头看这里为什么要有个光楔，主要就是为了把红光过蓝楔和蓝光过红楔的光滤掉，这样才能显示出两边分别上移和下移的效果。光楔本身并不能放大位移，只是通过两边方向不同来实现位移x2的效果。

那么回到我们最感兴趣的问题，这种测距方式的精度如何呢？同样的，我们先从光学的角度出发。如下图所示，从几何关系可以看出两边的位移差$d=\frac{D\Delta u}{f}$，其中D是镜头的通光直径，f是焦距，u是相距，$\Delta u$是焦平面和对焦屏的距离。里面用了一个近似是$f=u$。类似对旁轴的推导，我们从人眼的分辨率可以得到这里最小可分辨的$d$是0.015mm（记为$\delta$）。把公式变形可以得到$\Delta u$可分辨的最小值是$\frac{f\delta}{D}$。

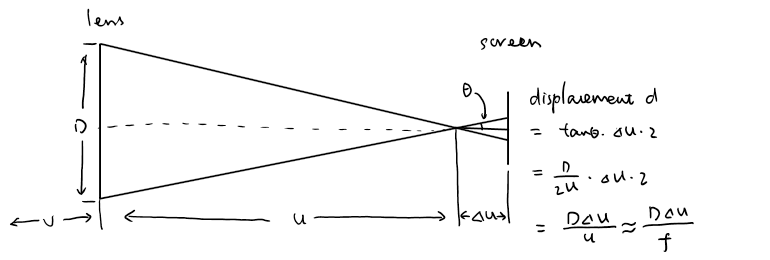
接着我们考虑高斯公式$\frac{1}{f}=\frac{1}{u}+\frac{1}{v}$，把公式变形可以得到$v=\frac{uf}{u-f}$，再次利用近似$f=u$可以得到$v=\frac{f^2}{\Delta u}$。再结合光圈的定义$N=\frac{f}{D}$，可以进一步化简得到我们所能测出来的最大的物距v是$\frac{f^2}{N\delta}$。如果我们用同样的50mm f/1.4的数据带进去可以得到此时测距的极限是120m。也就是说当物体从120m挪到200m，甚至挪到1500m远的时候，人眼看去裂像对焦屏上的像根本就没有移动位置，也就无从测距了。结合我们对视差测距的计算，同样的镜头在旁轴对焦器上的光学测距量程是1600m，从这里我们可以看出来，在不考虑机械精度而且用标头的时候，裂像对焦的精度其实是比不上旁轴的。但裂像有个好处是量程和焦距的平方成正比，我们换个索十万600mm f/4来看看。此时量程瞬间涨到了6000m，有钱真好。。

那么我们进一步看看机械精度。对裂像来说分析更简单，如果还是用50mm/1.4举例，对焦环拧比如120度镜头对焦距离从0.7m走到无穷远，也就是像距从53.8mm走到50mm。假设人手的精度是1度，那这里的$\delta$就是3.8/120=0.032mm。考虑到$\Delta v = \frac{f^2}{N\Delta u} - \frac{f^2}{N(\Delta u + \delta)}$，我们可以画出类似的误差曲线：

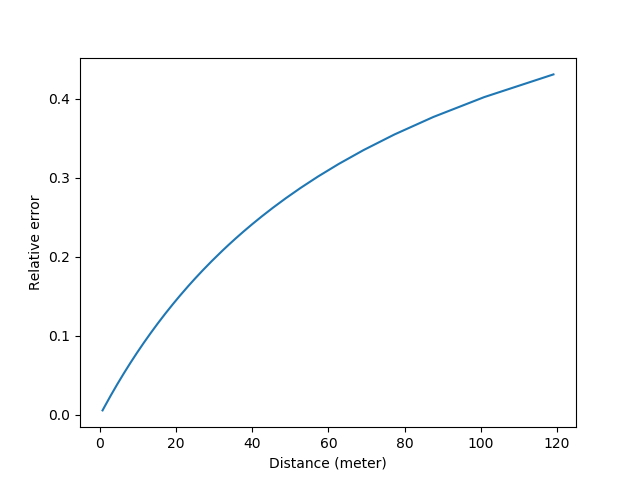
如果我们取5%相对误差的话，这个距离在6.0m。考虑到旁轴的5%误差测距量程是4.5m，综合来看，裂像因为能更有效地利用机械，测距精度比典型的旁轴略好。当然我们的估算都比较粗略，如果某一个参数变化的话，可能会得到相反的结果。

看完了黄斑和裂像，下面我们来看一下历史最悠久的峰值测距。在大画幅的年代，摄影师用的毛玻璃对焦其实就是峰值测距了。它的光路和裂像都是一样的，我们这里还是有弥散斑的直径是$d=\frac{D\Delta u}{f}$。但和裂像不同，因为人眼是很难看出来“一个点是不是一个点”的，而且这里也没有一个一根线断成两截的视觉辅助，所以大家对焦的方法一般是找一个点或者线，反复拧动对焦环使得它最清晰。这里的“最清晰”看的其实不是这个点最小，而是基本上大小不变，也就是一个一阶导的概念。也就是说，这个对焦方法的限制在，如果手转了对焦环，屏幕上的光斑大小看不出改变（半径改变量低于人眼分辨率），那么就可以认为达到了最大量程。峰值测距的几何分析图和裂像是一样的。

在对裂像的分析中我们有过计算，对于50mm f/1.4的标头，人手所能达到的$\Delta u$的最大精度是0.032mm，代入$d=\frac{D\Delta u}{f}$很容易得出此时d的变化值是0.023mm。但注意此时单边只会移动0.023/2=0.012mm，而人眼的分辨率约为0.015mm，所以此时机械精度不再是限制因素，光学成了更大的限制。用0.015mm反推$\Delta u$的精度，在最接近合焦的地方，要想产生肉眼可见的光斑变化，需要$\Delta u$变化0.042mm。也就是裂像分析中的$\delta=0.042mm$。代入误差公式$\Delta v = \frac{f^2}{N\Delta u} - \frac{f^2}{N(\Delta u + \delta)}$，可以得到这样的图表：

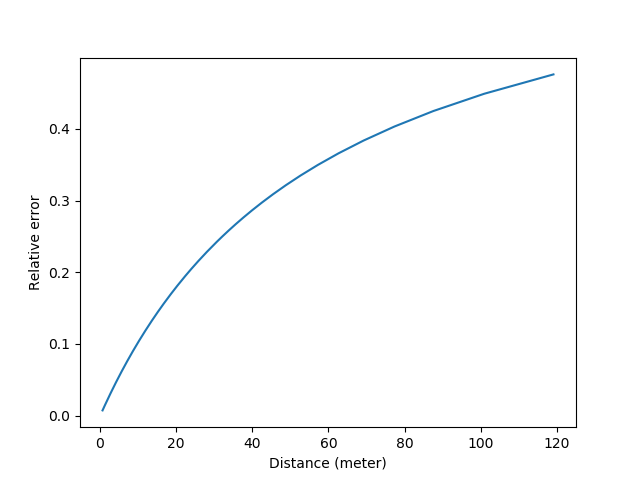
毛玻璃“峰值”测距的相对误差曲线

如果取误差5%处做量程的话，峰值测距+标头的量程是4.6m。由此可见裂像的设计非常有用，直接把量程增加了1/3左右。但要注意，传统的裂像和峰值都非常依赖于对焦屏的亮度。如果镜头的光圈太小，对焦屏比较暗的话，人眼的分辨率会远低于0.015mm。所以如果不改变镜头的通光口径，单纯增加焦距f的话，相对应的量程其实反而会下降。

在电子时代，传感器的分辨率远高于人眼的分辨率，而自动对焦马达的精度也远高于人手拧的精度。比如如果我们用a7r3的传感器来做峰值对焦，因为它的像素大小是4.5微米，远好于人眼15微米的分辨率，所以这里的\delta一下降低了3倍变成了0.013mm。此时的误差曲线变成了：

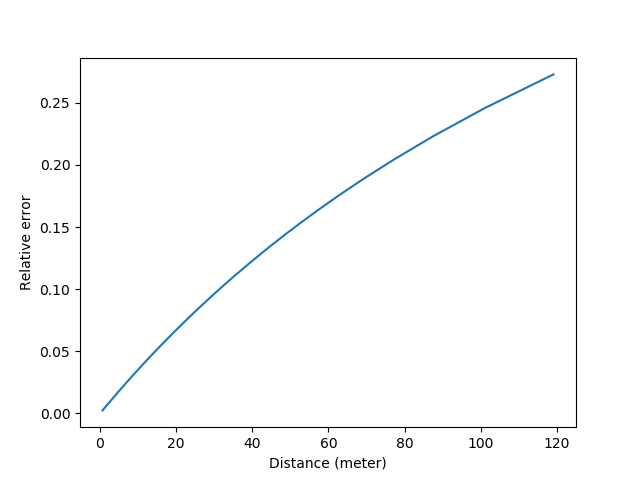
A7r3峰值测距的相对误差曲线

此时当物体在14.5m以外时，峰值测距仍然可以实现5%的误差。而且因为传感器ISO远高于废柴人眼，所以即使视野暗淡也没有关系。如果我们换成普通的长焦头135/4，则有效量程一下到了125m。由此可见数码化的有效。

但现实生活中的场景往往比这个模型要复杂。主要原因是不是所有东西都能找到一个光点给你慢慢对焦的。往往一虚焦，旁边的像素也糊了，大家彼此干扰直接完球。所以就需要一个算法来搞，这个就叫depth from defocus，对焦环从左到右打一遍，直接给你一个depth map。如下图所示。他们还造了一个专门的相机出来。顺便安利一下这个造相机的组，真的是非常硬核了。

Depth from defocus。图片来自http://www.cs.columbia.edu/CAVE/projects/depth_defocus/

在进入机器视觉时代以后，数码传感器的这种高精度的特征被迅速发掘。而且因为传感器直接就是一个阵列，所以往往能一把把整个场景中所有物体的距离全部测出来，也就是每个像素的都有自己的距离（叫做深度）。大概的说有以下三种方法比较流行：

• 双目测距，类似视差测距的数码版。但靠的不是人眼来检查合焦，而用的是电脑做像素匹配。如下所示。在这种情况下两张图象有很多良好的数学性质。比如会存在一个特别牛逼的矩阵叫做fundamental matrix。还有CMU的小哥写了一首歌叫The fundamenal matrix song: https://www.bilibili.com/video/av49649670。 有兴趣的同学可以去听听。

  

  典型的双目相机，可见不同的基线长度和镜头。图片来自https://nerian.com/products/karmin2-3d-stereo-camera/

• 散斑测距：就是流行的Kinect 1了。它的主要原理是用红外激光投射出一个已知的散斑图案。这个图案会随着目标物体的高低起伏而改变自己的形状。通过做一些像素匹配就可以得知物体的具体形状了。如下图所示。

  

  Kinect 1投射出的斑点图案。图片来自https://www.ign.com/boards/threads/on-the-differences-between-kinect-1-kinect-2-and-the-sony-camera.453537413/

• 激光测距：Kinect 2用的是time of flight，也就是流行的激光测距。它的基本原理就是光速x时间=距离。当然电子电路对极短时间（比如光走100m的距离只需要33ns）的测量还是比较昂贵，所以一般会把激光进行调制，然后测量相位的变化来反推时间进而反推距离。无人驾驶中常用的LiDAR也是同样的原理，只是因为需要360度的视野所以需要旋转激光器和传感器。但因为有了旋转的机械部件，刷新率受到了一定限制。所以现在逐渐兴起了相控阵LiDAR，通过电子系统而不是机械部件来实现信号的偏转。

  

  LiDAR扫描得到的结果。图片来自http://spicergroup.blogspot.com/2013/09/spicer-group-first-north-american-leica.html。

希望这些定量分析的过程和对机器视觉中深度测量的介绍能有所启发。