Computing Life

窄带摄影里有很多流行的调色方法，比如HOO，SHO。但拍多了不免腻歪，到处都是黄蓝哈勃色。同时很多目标用传统方法很难调色，比如乌贼星云，用SHO就是大黄配大蓝，HOO就是大红配大蓝，极高的饱和度让美学处理很难办。虽然可以通过一定程度的后期来对色调和饱和度拉曲线，但后期毕竟是有限度的，没办法在各个调色盘直接自由变换。有没有可能我们可以自己指定一组符合美学的调色盘，而不是用RGB=SHO这种饱和度拉到顶的方法来调色呢？这篇文章主要就来介绍这样的一种方法。

下图是一个成品例子，对乌贼星云，我们从黑客帝国中获得灵感，用带有警惕感的红色来给O为主的乌贼调色，而把背景缭绕的Ha+S云气用海蓝色来表现，以此来体现一只机械乌贼在海中警戒执行任务的观感。同时这两种颜色都不是正红正蓝，而是带有一点粉色的弱化版本，不会显得太城乡结合部。

这个是如何实现的呢？很简单，我们先介绍怎么做，然后介绍里面的数学原理。整个过程分为两步。首先我们先在PS里面选择想要的颜色。比如对H，我们想用海蓝色来表现，就在拾色器里面调出来我们想要的蓝色：

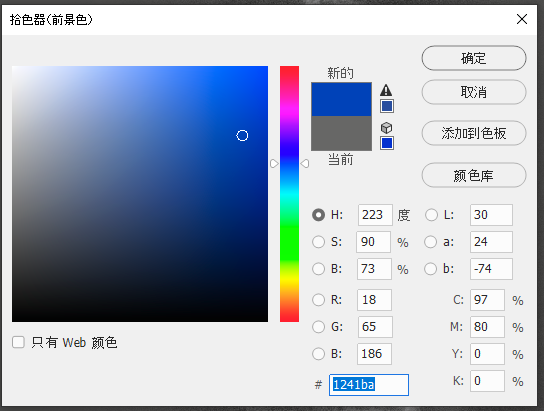
记下来它的RGB值是18, 65, 186。类似的，我们选用粉蓝色（56, 128, 235）来给S上色，选用带一点紫色的红色（235, 56, 174）来给O上色。

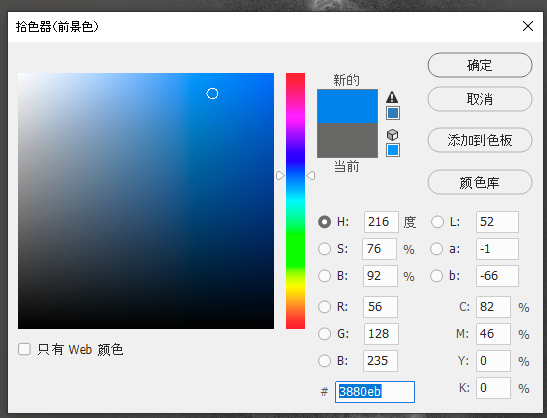
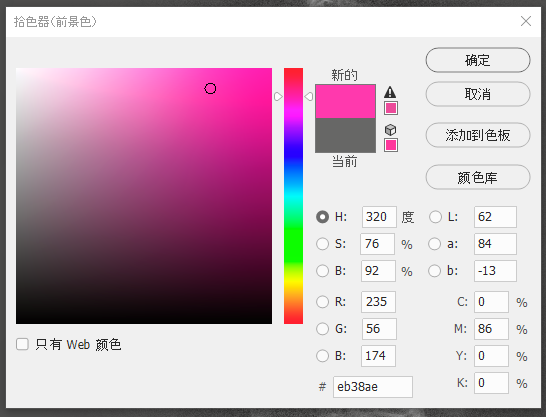
那么，我们如果把这些RGB列成一个表的话，是这样的：

    R   G   B
H   18  65  186
S   56  128 235
O   235 56  174

第二步来了，下面我们竖着看这个表，然后把每一列的内容和HSO乘起来然后加起来，就可以直接得到PixelMath的公式了。比如我们看R这一列，HSO对应的三个数是18, 56, 235。那么R通道的公式就是18*H+56*S+235*O。 但此时有个问题，是这样算出来的结果会超出0和1的范围，所以需要做一个简单的归一化。也就是出来的结果还要除以这三个数的和，也就是R的公式是(18H+56S+235*O)/(18+56+235)。如果我们对G和B也做同样的处理，最终的公式是：

• R: (18*H+56*S+235*O)/(18+56+235)
• G: (65*H+128*S+56*O)/(65+128+56)
• B: (186*H+235*S+174*O)/(186+235+174)

把它输入到PixelMath里面，出来的图像是这样的：

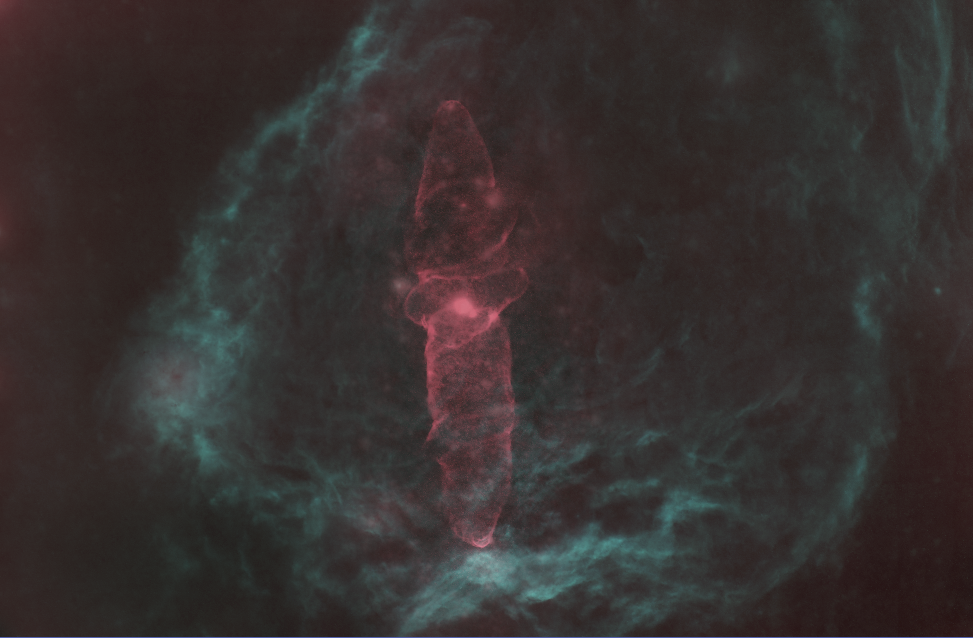
可以看到红色基本上就是我们挑选的颜色。为什么背景和挑选的颜色不一样，主要是因为背景同时有H有S，两种蓝色一混合就变成了这种青色。不过没关系，我们在CurveTransform里面稍微拉一下色调，饱和和明度，就可以得到上面的成图了。

拓展出去，其实RGB图也完全可以这么玩，只要当做伪色调色就好。甚至多于3个通道的调色也可以套用同样的方式解决。只要把这个表拓展到4行5行就好。总之这种方法通过简单的数学（不超过加减乘除），提供了一种系统性，可拓展，可控制的调色方法。

如果感兴趣的话可以继续看一下原理。我们现在面临的问题是线性代数里面比较典型的线性空间投影问题。我们有三组正交基H, S和O，张成了一个线性空间。这个空间里面的任何一个向量(H, S, O)都有自己的坐标，这个坐标的三个值就是HSO三个通道在这个像素的亮度。然后现在的问题是，如果我们想要把这个线性空间投影到另一组基上，应该怎么算出来(H, S, O)这个点在新空间下的坐标(R, G, B)。一般情况下，这组新的基向量应当是正交的，也就是SHO调色，HOO调色等情况。但在我们的例子里，我们放宽了这个条件，让颜色可以不正交，但还是用同样的方法来投影。所谓投影，根据线性代数，其实就是用一个变换矩阵去和待变换的向量(H, S, O)去做矩阵乘法，然后这个变换矩阵也很简单，就是把三个新的基罗列成一个矩阵就好。那么问题就很简单了，一个公式就可以表达：

$$ \text{RGB}^T = R \cdot \text{HSO}^T $$

R是变换矩阵。或者如果我们把这个矩阵展开，就是：

$$ \begin{bmatrix} R \ G \ B \end{bmatrix} = \begin{bmatrix} H_R & S_R & O_R \ H_G & S_G & O_G \ H_B & S_B & O_B \end{bmatrix} \cdot \begin{bmatrix}H \ S \ O\end{bmatrix} $$

也就是我们上面列的那个表格。这里只是转置了一下，第一列是H对应的RGB值，而不是第一行。以此类推。所以用简单的线性代数，我们就可以定量精确地控制SHO的出图，甚至因为这里不要求R是正交矩阵，可以提供多于三通道的投影。